Vibrations
I found that a lot of people, including myself, were having trouble understanding and graphing a SDOF (single degree of freedom) system used in one of our earlier Vibrations homeworks. I decided to write a tutorial because I know I was looking for one at the time of the assignment and I was having difficulty finding a good explanation. Here is an image of the final result of this tutorial.
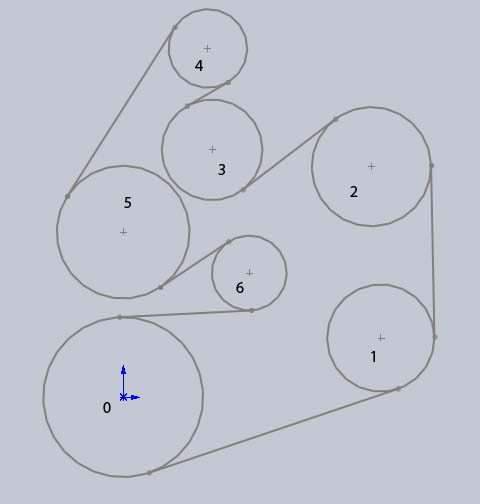
The final project for this class involved a MDOF (multiple degree of freedom) system. This particular system came from the belt of a Ford engine. If you want to know how to graph the frequency response of a MDOF system you can go here for my MDOF tutorial.
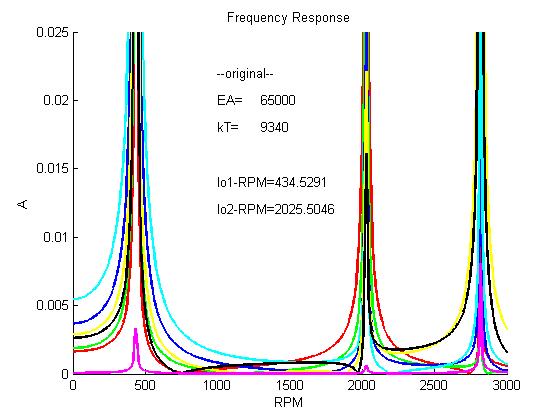
The problem was stated that two of the system's natural frequencies (434 RPM and 2025 RPM) were inside the normal operating range of the engine. The goal then was to move these two frequencies out of the normal operating range. Here is an image of the frequency response of the original system.
The system was then changed so that the lower frequency of 434 RPM was lowered to 362 RPM and the upper frequency of 2025 RPM was raised to 2530 RPM. Here is a plot of the frequency response of the new system.
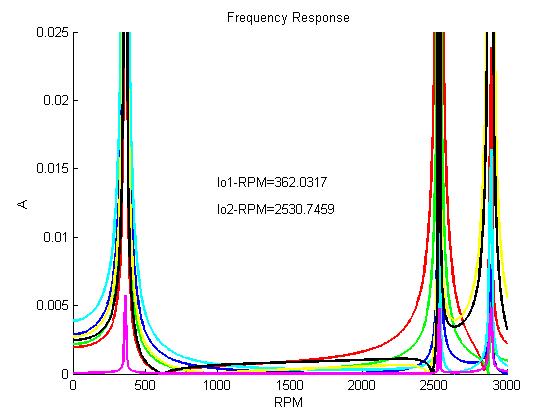
This optimization of the system was done initially by examining the relationships between all of the variables and choosing values that optimized the system.
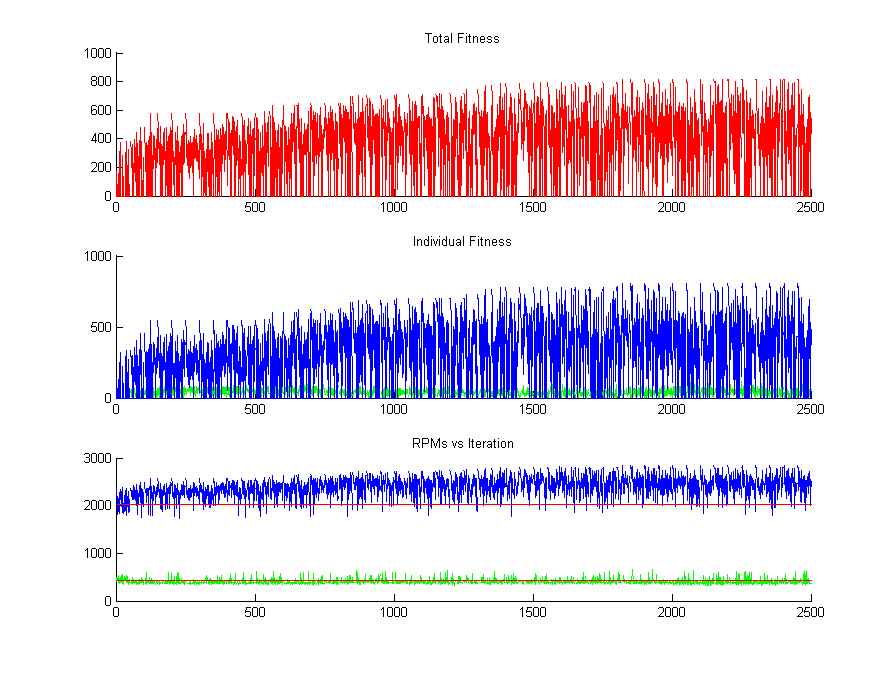
Because of my fascination with Genetic Algorithms at that time, I wrote my own GA to solve this optimization problem. However now that I understand more about the theory of optimization I know that GAs are not well suited to this problem.
The plot below shows how over several iterations of the GA the "fitness" of the solution increases. In the bottom two subplots you can see the blue line (representing the upper problematic frequency) and the green line (representing the lower problematic frequency) as it changes in the GA. A blue point above the flat red line adds "fitness" and a green point below the other flat red line also adds "fitness". This is a multi-objective optimization problem and so I decided to assign equal weight to both of the "fitness" values. This causes the solution to focus on improving the blue (upper frequency).