Test Case: Bio-Engineering Simulation
Someone came to me with a Bio-Engineering problem that involved a set of non-linear differential equations. He wrote a program in MATLAB that was using computational methods (Euler Method) to solve the problem. His program worked well, but the program took around 30 minutes to test 30^4 combinations of parameters over 1000 time steps. So I gave him some advice about writing programs that will execute quickly. After giving my initial advice though I continued to research and test various methods of writing optimized code. In the process I found a few surprises and learned a lot about optimizing code.
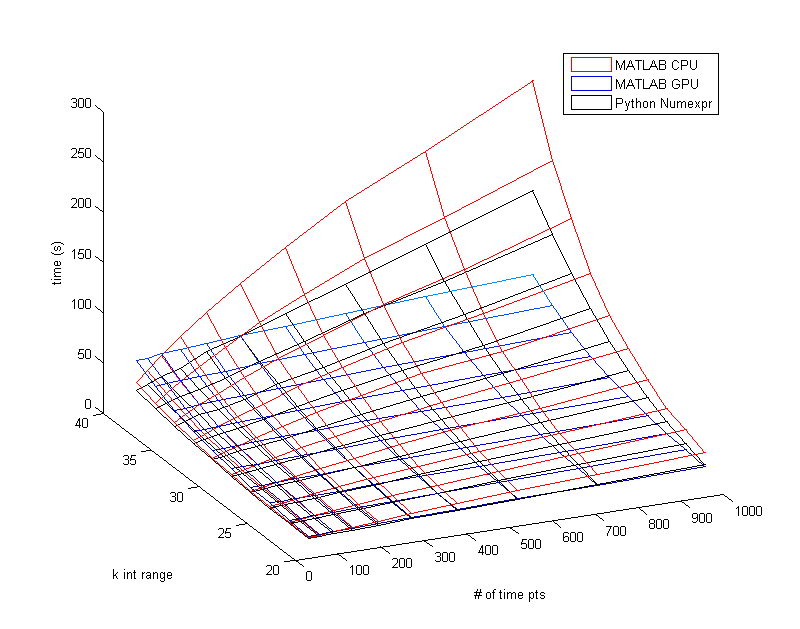
However one thing that didn't surprise me is how powerful a GPU (Graphics Processor) is at crunching through parallel for-loop code. Below is a figure from MATLAB to demonstrate how much quicker the GPU is than the CPU in MATLAB (the lower time/z-value is better). I was now able to do what used to take 30 minutes in a little under 60 seconds on the GPU.
Here is a chart of the average results for 8 different setups running the 30^4 combinations over 1000 times steps. The original setup took over 30 minutes but was running on MATLAB and not using pre-allocated arrays. Pre-allocating the arrays clearly makes a huge difference when dealing with large sets of data, but the program can still be improved from there.
Using a for-loop on pre-allocated arrays does not take advantage of the fact that most computers have multiple cores on their CPU. When you replace a for-loop with vectorized code you cut the program's execution down significantly by using all of your cores. Using a parfor-loop (parallel for-loop) instead can get similar results because this method also uses all of the cores. Additionally it could connect to networked clusters of computers to use even more cores. For my testing though the parfor-loop was not connected to any networked clusters and was only using my local cores. Using my GPU with MATLAB to run vectorized code is similar to using vectorization on the CPU but the GPU has even greater performance. This can vary of course, the GPU includes high overhead cost but my GPU has 336 cores compared to my CPU which only has 4.
I switched over to Python (using version 2.7 on Windows 7)to see how it would perform. Python requires Numpy (Numerical Python) to use vectorization, but unfortunately vectorized Numpy is even slower than non-vectorized MATLAB. From what I've read they both use the same lower level code so I'm not sure why there is such a big difference. Surprisingly a Python module called Numexpr (which also uses my CPU and its 4 cores) is just as fast as my GPU in MATLAB. I then tried these two implementations of Python but now I was using the Ubuntu OS. Now vectorized Numpy ran about 2x faster than it did in Windows and Numexpr took way too long. I'm not sure what the causes of these changes are.
Below is a Mesh plot of MATLABs vectorization on the CPU vs. vectorization on the GPU. The k int range just means how many combinations were tested, but the value needs to be raised to the 4th power. So a k int range of 30 means 30^4 different combinations of parameters to be tested. Only in the very low time point ranges does the CPU outperform the GPU. It is important to remember that not all computers will have GPUs that have this much of an advantage, and that not all situations will benefit from the GPU.
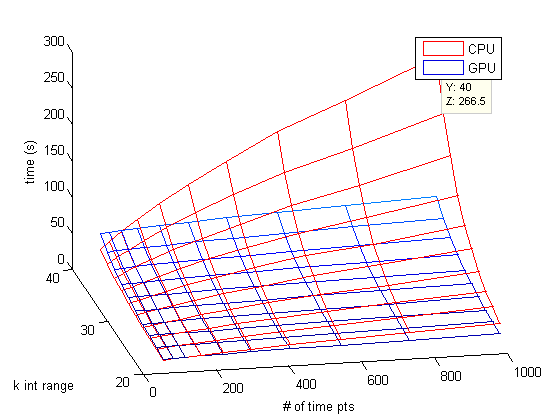
Moving from 30^4 combinations to 40^4 combinations shows the dominance of using the GPU in MATLAB. Numexpr in Python still seems to be the fastest method to use on a computer without a powerful GPU. Of course you could always skip these higher-level languages and use a slightly lower-level C or C++. There are even methods available where you can write C code in your higher-level MATLAB (MEX Files) or Python (Cython or Scipy Weave). However the truth is that when you vectorize your code you are essentially asking MATLAB and Python to turn your vectorized code into very efficient low-level algorithms. These algorithms are often faster than anything you could easily write yourself.